This week I’m attending a conference in Strasbourg. While following the opening plenary, I log in to the server, on which my world record computation of pi is running. My interest in the ongoing presentation diminishes rapidly, when I realise that the computation of the hexadecimal digits of pi finished yesterday. Now it will turn out, whether the computation was correct or whether an undetected error, e.g. in the massive disk I/O, spoiled the computation. Y-Cruncher has built-in redundancy checks, but there is still a chance for a computation to end with a wrong result. In this case, the work of the last three months was a waste of time.

Bellard’s formula for the n-th hexadecimal digit of pi
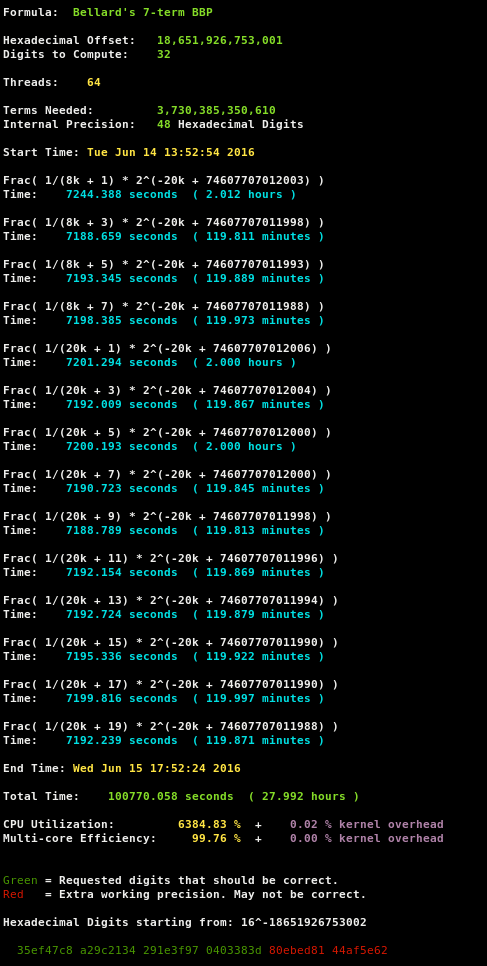
bellard
Computation of the last hexadecimal digits using Bellard’s formula.

To verify the correctness of the hexadecimal digits of pi, y-cruncher implements Bellard’s formula. This equation can be used to compute the n-th hexadecimal digit of π without the need of computing the preceding digits. The formula is a variant of the Bailey-Borwein-Plouffe formula, which was discovered in 1995. The calculation requires much less resources than the full computation, so I could run it in June even before the 144 TB storage was ready. The algorithm run for one day and computed the 32 hexadecimal digits of pi starting at an offset of 18’651’926’753 001 to be 35ef47c8 a29c2134 291e3f97 0403383d.

 

Verification of the hexadecimal digits of pi

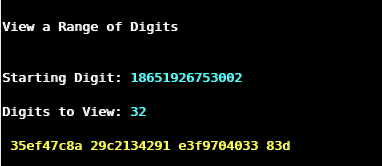
After having compiled y-cruncher’s digit viewer, I’m in the position to extract the last hexadecimal digits of the full computation. On my screen, the following numbers appear:

last hexadecimal digits of pi

Indeed, these are the same digits as computed with Bellards’s formula. Thanks to God, the two results agree! I’m relieved that all the effort was not in vain. Now, the computation can enter its final stage: the conversion of the hexadecimal to decimal digits. If you are interested to get a copy of the full 18.6 trillion hexadecimal digits of pi, feel free to contact me.