The formula used by y-cruncher to compute π is called after the Chudnovsky brothers, two mathematicians living in the United States. In 1989 they published the following formula:
$$\Large \frac{1}{\pi} = \frac{\sqrt{10005}}{4270934400} \sum_{k=0}^{\infty}(-1)^k\frac{(6k)!}{(k!)^3(3k)!}\frac{(13591409+545140134k)}{640320^{3k}}$$
Thanks to the denominator of the last term, the sum converges very rapidly. With every term one gets 14 more correct decimal digits of π! So for our world record computation of 22 459 157 718 361 digits we only need to compute 1 583 677 621 196 terms.
The following python script implements the Chudnovsky formula and prints the deviation from the precise value of π. As you can see, 7 terms are sufficient to get the first 100 digits of π.
Result:
1 terms: Delta = -5.90307941897917e-14
2 terms: Delta = 3.0784780427869695e-28
3 terms: Delta = -1.7205202595330623e-42
4 terms: Delta = 1.0002815712846047e-56
5 terms: Delta = -5.9591518750910765e-71
6 terms: Delta = 3.609068527148001e-85
7 terms: Delta = -9e-100
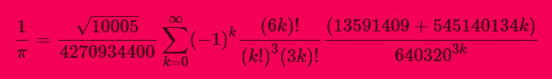




Comments by Pipi